In this article, we’ll look at Graduate Admissions problem and try to solve it with Artificial Neural Networks. As this is a regression problem, we’ll mostly deal with numerical data.
Overview
This dataset is created for prediction of Graduate Admissions from an Indian perspective. The dataset contains several parameters which are considered important during the application for Masters Programs.
The process of graduate admissions is a pivotal step for both aspiring students and academic institutions. The quest to forecast a candidate’s likelihood of acceptance into graduate programs has been a longstanding challenge, but with the advent of Artificial Neural Networks (ANN), a new era of predictive analytics has dawned. In this article, we’ll explore how ANN can be leveraged to predict graduate admissions, unraveling insights from the dataset available on Kaggle. Here our only goal is to understand the working of neural networks with regression problems.
What is Graduate Admission Prediction
Predicting graduate admissions involves building a model that can estimate the likelihood of a student being admitted to a graduate program based on various factors such as academic performance, standardized test scores, letters of recommendation, and statement of purpose. It’s a regression problem where the goal is to predict a continuous value representing the likelihood of admission.
Exploring the Dataset
The dataset sourced from Kaggle contains information about various parameters believed to influence graduate admissions, including:
- GRE (Graduate Record Examination) Scores
- TOEFL (Test of English as a Foreign Language) Scores
- University Rating
- Statement of Purpose and Letter of Recommendation Strength
- Undergraduate GPA (Grade Point Average)
- Research Experience
- Chance of Admit (Target Variable)
Building an Artificial Neural Network
Using the powerful tools provided by libraries like Keras, we can construct an ANN tailored for regression tasks. Here’s a step-by-step guide to building the model:
- Data Preprocessing: Load the dataset and preprocess it by handling missing values, scaling numerical features, and encoding categorical variables if any.
- Model Architecture: Design the architecture of the neural network. For regression tasks, a simple architecture with input and output layers suffices. We’ll utilize densely connected layers with appropriate activation functions.
- Compilation: Compile the model by specifying the appropriate loss function and optimizer. Since this is a regression problem, mean squared error (MSE) is commonly used as the loss function.
- Training: Train the model on the training data. Adjust hyperparameters such as the number of epochs and batch size to optimize performance.
- Evaluation: Evaluate the trained model on the test data to assess its performance. Metrics such as mean absolute error (MAE) and root mean squared error (RMSE) provide insights into the model’s accuracy and generalization capabilities.
The ‘Chance of Admit‘ is our target column and its values are in decimal numbers, so it is a regression problem. Rest of the columns are input columns.
Code the Model For Neural Network
Lets first get all data and look for preview of the data.
import pandas as np
import tensorflow
from tensorflow import keras
from tensorflow.keras import Sequential
from keras.layers import Densedf = pd.read_csv('/kaggle/input/graduate-admissions/Admission_Predict_Ver1.1.csv')
df.head()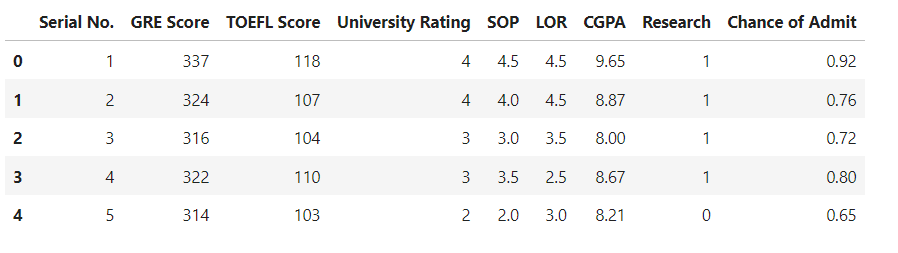
As we can see we have 500 records and 9 columns. We can check it using below code.
df.shapeLets check for missing values in dataset and also the data types.
df.info()As there is no missing values in dataset and no duplicate records as well, we can go ahead and remove the unnecessary columns.
df.drop(columns=['Serial No.'], inplace=True)Now we have only 7 input columns and 1 target column.
We need to divide the data into training and testing sets using train test and split method.
X = df.iloc[:, 0:-1]
y = df.iloc[:,-1]from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state = 1)As our data far away from each other, means some values are very small and some are very big numbers. So we need to scale our input dataset. We’ll use the min-max scalar, as there is upper limit and lower limit to some of the values in dataset.
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)After doing this we’ll get a transformed Numpy array with scaled values.
Build Neural Network Model
model = Sequential()
model.add(Dense(7,activation='relu', input_dim=7))
model.add(Dense(7,activation='relu'))
model.add(Dense(1,activation='linear'))In above code we have 1 input layer with 7 inputs, two hidden layers with ‘relu‘ as activation function and 1 output layer with only one node and activation function as linear. Always remember that whenever we deal with a regression problem the activation function of output layer should be linear.
Now lets check the summary.
model.summary()
As we can see there are total 64 trainable parameters.
Now lets compile our model and train it using fit() method.
model.compile(loss='mean_squared_error',optimizer='Adam')
history = model.fit(X_train_scaled,y_train,epochs=50,validation_split=0.2)In above code we have selected the loss function as ‘mean_squared_error‘, and running 50 epochs on scaled input data.
We can now predict the test data and check for r2 score.
y_pred = model.predict(X_test_scaled)
form sklearn.metrics import r2_score
r2_score(y_test, y_pred)So our r2 score is 0.647, which is not so good but we can improve it anytime by tuning the parameters. Lets plot the graph to compare loss and check for overfitting problem.
import matplotlib.pyplot as plt
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])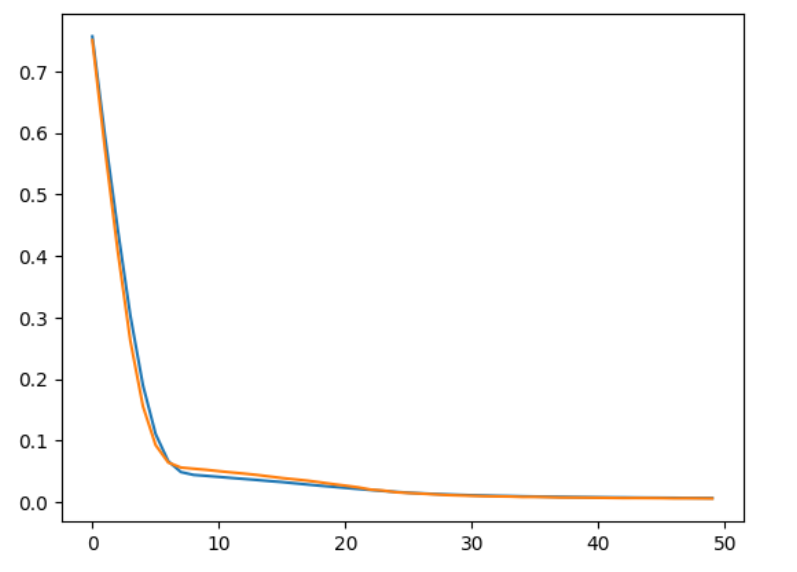
As we can see there is not much of the overfitting problem. Full code is here.
Predicting graduate admissions using Artificial Neural Networks opens up new possibilities for streamlining the admissions process and providing valuable insights to both students and academic institutions.

